M2DPCA和NFA相结合的人脸识别方法
人们在日常生活中最常用的身份认证手段就是人脸识别，其也是当前模式识别中一个最热门的研究课题。人脸识别就是将动态捕捉到的人的面部与预先录用的人脸库中的人脸进行比较识别。现已经广泛地应用于国家安全、刑事侦破等领域。人脸与指纹、虹膜等其他生物特征一样与生俱来，具有唯一性和不易被复制的良好特性；且人脸识别具有可以远距离采集人脸图像，是一种非接触性的技术，具有非侵犯性的特点， 但是人脸图像的特征空间分布非常复杂；另外，还不能找到完全可分的特征映射和相应曲面进行分类识别。
特征提取是人脸识别过程中的关键问题。在各种特征提取方法中，Belhumeur 等人提出的Fisher 脸（Fisherfaces）方法和Turk 等人提出的特征脸方法（Eigenfaces）方法[3]是两种应用最为广泛的算法。Fisher 脸方法是通过线性判别分析（Linear Discriminant Analysis，LDA）寻找使类内距和类间距最小比值的投影方向来获取判别信息， 是一种有监督的方法。
使用LDA 方法进行人脸识别时，可能遇到两大问题：1）小样本问题（Small Simple Size，SSS）；2）边缘类的存在造成投影空间中近邻样本的重叠。且由于LDA 方法中的类间散布矩阵Sb的秩最多有c-1 个，因此，特征向量最多有c-1 个。对于高维数据，要很好地区分各个类，只有c-1 个特征是不充分的。此外，类内散布矩阵只考虑了类的中心，没有考虑类的边界结构， 而这些边界结构已经证明了在分类时有很大作用的，这些问题导致了LDA 方法性能的不稳定。为解决这些问题，Li等人于2009 年提出了非参数子空间分析方法（Non-parametricSubspace Analysis，NSA）。主成分分析（Principal ComponentAnalysis, PCA）在做特征提取时提取的是全局特征，识别效果往往不是很理想, 而实际上当人脸表情和光照条件变化时， 仅部分人脸区域变化明显， 而其他部分变化不大， 甚至无变化。M2DPCA 方法则是对PCA 算法的改进，它是对划分后的子图像进行鉴别分析， 可以捕捉人脸的局部信息特征，有利于识别。
由于NSA 方法中的类内散布矩阵Sw 仍然和LDA 的一样，这样可能会影响识别效果；且NSA 方法计算类间散步矩阵没有考虑到不同的KNN 点有助于构建不同的类间散布矩阵。Li 等人提出了非参数特征分析（nonparametric featureanalysis，NFA）方法，本文在降维方面作了改进即先对图像矩阵分块并采用2DPCA 进行特征预提取， 得到替代原始图像的低维新模式后对其施行NFA 方法。在ORL 人脸库及XM2VTS人脸库上验证了该方法， 其识别性能优于LDA 方法、NFA方法。
1 M2DPCA+NFA
1.1 基于M2DPCA 的特征提取
设模式类别有C 个：C1，C2，…，CC，第i 类有ni个样本。训练样本图像为：
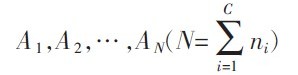
训练样本A i的p×q 块图像矩阵表示为：
其中每个子图像矩阵（Ai（j））k，l（i=1，2，Λ，c；j=1，2，Λ，ni；k=1，2，Λ，p；l=1，2，Λ，q）是m1×n1（m1×p=m，n1×q=n）矩阵。
训练样本的总体散布矩阵为：
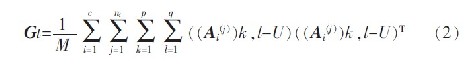
其中M=Npq 表示训练样本子图像矩阵总数：
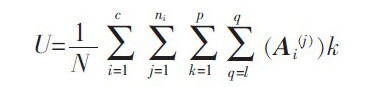
l 是所有训练样本子矩阵的总体平均值，我们很容易就能得出Gt 为m1×m1的非负定矩阵。
定义准则函数：
Gt 的前t 个最大特征值所对应的标准正交的特征向量Z1，Z2，…，Zt为最优投影向量组，最优投影矩阵Q=[Z1，Z2，…，Zt]。由此可得训练样本在Q 上投影的特征矩阵：
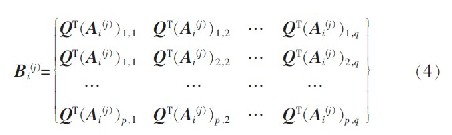
值得注意的是：在对原图像施行模块化2DPCA过程中，当确定图像分块后，投影轴个数t 的取值就决定了特征矩阵Bi（j）的维数。若t 值取小了， 特征矩阵中会遗失许多不利于稍后分类的鉴别信息，然而t 值取大了， 则特征矩阵中又将存在大量不利于降维的冗余信息。t 可按如下方法取值，先求总体离散矩阵Gt的特征向量，按降序排列为：λ1，λ2，…，λme，令
l=1，2，Λme，则t 取使得min{ηl /ηme≥1-ε（0<ε≤0.01）}成立的l 值。
1.2 基于NFA 的特征提取
令（xi（j））k，l=Vec（Bi（j））k，l，则（xi（j））k，l∈R m1 n1 ，k=1，2，…，p，l=1，2，…，q；第i 类第j 个图像样本的子图像矩阵的均值为：
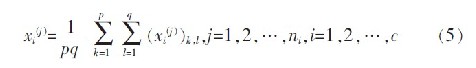
定义新的类间散布矩阵：
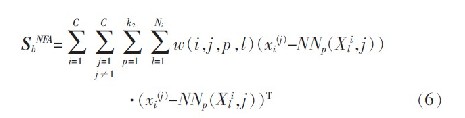
新的类内散布矩阵：
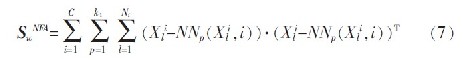
其中，NNk（xi（j），l）为类l 到xi（j）的K 个最近邻的集合，式（6）中权值w（i，j，l）为：
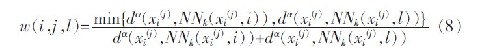
式（7）中α 是一个正参数，可以控制关于距离比的权值变化速度，d（xi（j） ，NNk（xi（j） ，l））是xi（j）到集合NNk（xi（j） ，l）距离。
于是，相应的准则函数为：
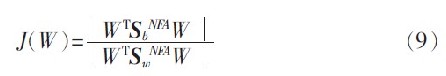
取特征方程SbNFAω=λSwNFAω 的前d 个最大特征值对应的特征向量作为最优鉴别向量。
2 实验结果与分析
2.1 在ORL 人脸库上的实验
ORL 人脸库中共有40 人在不同时期不同状态下拍摄的10 张照片，每张照片的分辨率均为112×92，照片有侧面、正面；表情严肃、表情放松；睁眼、闭眼；微笑、不笑；戴眼镜、不戴眼镜等诸多差别。以下是取自人脸库的一组照片：
图1 ORL 人脸库
表1 给出了对原始图像矩阵进行8×4、16×4 即图像子矩阵大小分别是14×23、7×23 两种分块后与LDA、NFA 方法对比的结果。分类器为最小距离分类器[8]。
本文中取ε≤0.01。由表1 数据可以看出，8×4 分块和16×4 分块在识别率方面均要优于LDA 和NFA 方法。
2.2 在XM2VTS 人脸库上的实验
XM2VTS 人脸库中共有295 人在不同环境不同表情下拍摄的8 张照片， 每张照片的分辨率均为55×51， 照片包括低头、抬头，戴眼镜、不戴眼镜，表情愤怒、表情平和，侧脸、正脸，有妆、无妆等各种差异。以下是取自人脸库的一组照片：
图2 XM2VTS 人脸库
本实验中以每组前4 张作为训练样本， 后4 张作为测试样本。总的训练样本和总的测试样本均为1 180 张。实验的结果， 正确识别率的对应关系见表2，表2 给出了对原始图像矩阵进行11×3 和5×17 即图像子矩阵大小分别是5×17 和11×3 两种分块后与LDA、NFA 方法对比的结果。分类器为最小距离分类器。
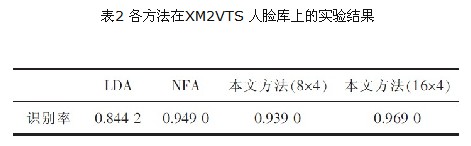
由表1 和表2 的数据可以看出， 在识别率方面本文方法均要优于LDA 和NFA 方法。具体言之， 在ORL 数据库中，LDA 方法结果是93.50%， 而NFA 方法的结果是98.00%，新方法的最高识别率达99.00%。在XM2VTS 数据库中，LDA 方法的结果是84.42%，NFA 方法的结果是94.90%，新方法的最高识别率为94.83%。本方法在ORL 人脸库上效果较为明显。
LDA 方法和NSA 方法在处理数据时只对一维数据进行处理，大大增加了计算量，容易出现“小样本问题”。而本文的方法首先使用模块化2DPCA 对二维数据进行特征提取，考虑到了图像的局部特征，而且图像维数的降低，减少了计算量。在此基础上转化为一维数据使用NSA 方法，考虑到了类内及类间的差异性，可以取得更好的识别率。
3 结论
本文在NFA 的基础上提出了M2DPCA 和NFA 相结合的一种新的人脸识别方法。首先利用模块化2DPCA 对原始数据进行预处理，再对得到的新的图像样本实行NSA 判别分析，这样做的优点是能够抽取到图像的局部特征，反映图像之间的差异的同时，亦能降低维数，使计算简单，得到更高的识别率。但研究发现， 对同一个库中的原始图像分块方法的不同，识别率一般都不同，因此，如何分块才能得到更高的识别率有待于进一步研究。
M2DPCA和NFA相结合的人脸识别方法
公司简介 
推荐产品
QQ在线咨询： 524736481 、 2850673955 、 2850673956 、 302753320 、 2850673950 、 2850673951
